$\require{cancel} \newcommand{\Ket}[1]{\left|{#1}\right\rangle} \newcommand{\Bra}[1]{\left\langle{#1}\right|} \newcommand{\Braket}[1]{\left\langle{#1}\right\rangle} \newcommand{\Rsr}[1]{\frac{1}{\sqrt{#1}}} \newcommand{\RSR}[1]{1/\sqrt{#1}} \newcommand{\Verti}{\rvert} \newcommand{\HAT}[1]{\hat{\,#1~}} \DeclareMathOperator{\Tr}{Tr}$
Grover's Algorithm 4-item Trial¶
First created in August 2018
With reference to Grover's Algorithm, we are doing a trial run with a 4-item list.
This exercise is motivated by the need to visualise the Grover's Algorithm and to translate the mathematics to the circuit.
Recap¶
Inputs:
- $n$ qubits
- An unstructured list of $N=2^n$ items
- A winning state $\Ket w$
- Associated with to $\Ket w$ an oracle, a unitary operation $U_f$, where $U_f\Ket w=-\Ket w$, and $U_f\Ket x=\Ket x$ where $\Ket x\ne\Ket w$.
Process:
A uniform superpostion $\Ket s={1\over\sqrt N}\sum_{x=0}^{N-1}\Ket x$, which is used as the initial state.
A "reduction" of $\Ket s$ with all basis vectors but $\Ket w$: $\Ket{s'} ={1\over\sqrt{N-1}}\sum_{x=0,x\ne w}^{N-1}\Ket x =\sqrt{N\over N-1}\Ket s-\sqrt{1\over N-1}\Ket w ,~$ and is orthogonal to $\Ket w$ as $\Braket{s'\Verti w}=0.$
$\Ket s=\alpha\Ket{s'}+\beta\Ket w,~$ where $\alpha=\sqrt{1-{1\over N}}~$ and $~\beta=\sqrt{{1\over N}}~.~~$
Reflection on $\Ket w, U_f=2\Ket{s'}\Bra{s'}-I.$
Reflection on $\Ket s, U_s=2\Ket s\Bra s-I.$
$\Ket{\psi_t}=\left(U_sU_f\right)^t\Ket s\approx\Ket w,$ when $t\approx\sqrt N$.
Reverse Engineering from IBM Q Experience¶
In IBM Q Experience, they illustrated the circuit like this:
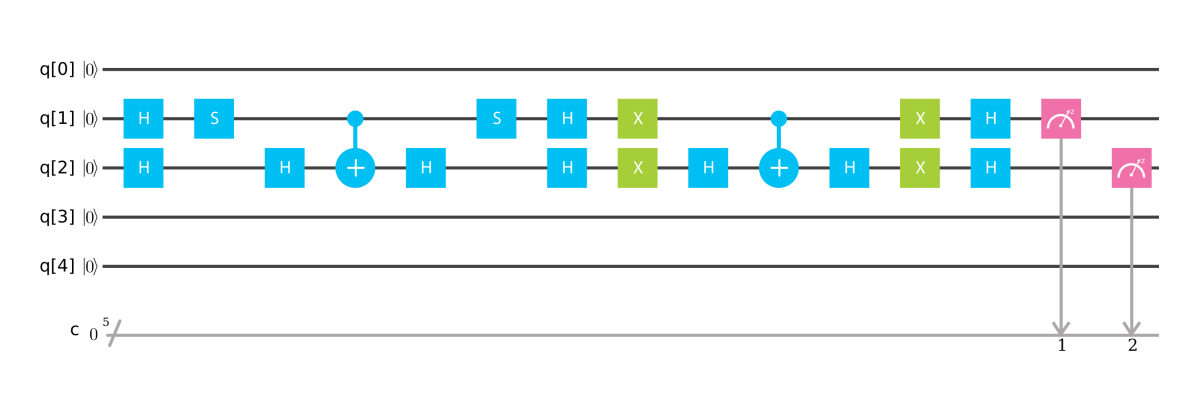
images/0qbyzkc53sj1yvi.png
They implemented the above illustration in the following way without much explanation. It skipped q[0] supposingly due to some machine restrictions.
Needs these assumptions to make sense out of it:
- $q_1\otimes q_2$. i.e. MSD on q[1], LSD is on q[2].
- The first (left most) $H\otimes H$ is a preparation.
- $U_f$ is from $S\otimes I$ to $S\otimes I$ inclusively.
- $U_s$ is from the second $H\otimes H$ to the third $H\otimes H$ inclusively.
- There is only one iteration.
- There is no finalisations.
Grover N=2 A=10

Note: The 4-item list is a special. It reaches unity probability in a single iteration as $\theta=\pi/6,~$ so $\theta_t=(2t+1)\theta=\pi/2$ when $t=1$.
Let us first prove that the IBM Q Experience implementation is correct ($q_1\otimes q_2$).
$U_f$ Circuit¶
Let us start with the above example of $\Ket w=\Ket{10}$.
$U_f =(S\otimes I)(I\otimes H)cX(I\otimes H)(S\otimes I) =(S\otimes H)cX(S\otimes H) .$
$cX= \begin{bmatrix} I&0\\ 0&X\\ \end{bmatrix} ,~ (S\otimes H) =\begin{bmatrix} H&0\\ 0&iH\\ \end{bmatrix} ,~ cX(S\otimes H) =\begin{bmatrix} H&0\\ 0&iXH\\ \end{bmatrix} ,~ U_f =\begin{bmatrix} H^2&0\\ 0&-HXH\\ \end{bmatrix} =\begin{bmatrix} I&0\\ 0&-Z\\ \end{bmatrix} =\begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\ 0&0&0&1\\ \end{bmatrix} .$
So the $U_f$ does encode a $\Ket{10}$.
All things covered, given $SS=Z,~~HXH=Z,~~cZ=H(cX)H,~~~SZS=I$:
$\begin{array}{lllr} U_f & \text{ Step 1 } & \text{ Step 2 } & \text{ Encoding } \\\hline (S\otimes S)cZ(S\otimes S) & \begin{bmatrix}S&0\\0&iS\end{bmatrix} \begin{bmatrix}I&0\\0&Z\end{bmatrix} \begin{bmatrix}S&0\\0&iS\end{bmatrix} & -\begin{bmatrix}-Z&0\\0&I\end{bmatrix} \sim\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} & \Ket{00} \\ (I\otimes S)cZ(I\otimes S) & \begin{bmatrix}S&0\\0&S\end{bmatrix} \begin{bmatrix}I&0\\0&Z\end{bmatrix} \begin{bmatrix}S&0\\0&S\end{bmatrix} & \begin{bmatrix}Z&0\\0&I\end{bmatrix} =\begin{bmatrix}1&0&0&0\\0&-1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} & \Ket{01} \\ (S\otimes I)cZ(S\otimes I) & \begin{bmatrix}I&0\\0&iI\end{bmatrix} \begin{bmatrix}I&0\\0&Z\end{bmatrix} \begin{bmatrix}I&0\\0&iI\end{bmatrix} & \begin{bmatrix}I&0\\0&-Z\end{bmatrix} =\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&1\end{bmatrix} & \Ket{10} \\ (I\otimes I)cZ(I\otimes I) & \begin{bmatrix}I&0\\0&I\end{bmatrix} \begin{bmatrix}I&0\\0&Z\end{bmatrix} \begin{bmatrix}I&0\\0&I\end{bmatrix} & \begin{bmatrix}I&0\\0&Z\end{bmatrix} =\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&-1\end{bmatrix} & \Ket{11} \end{array}$
$U_s$ Circuit¶
First, we need to generate $\Ket s$, which is all combination of $\Ket0$ and $\Ket1$, multiplied by ${1\over\sqrt N}={1\over\sqrt{2^n}}$. It can be constructed by an $H$ gate on all qubits in reset state.
$\Ket s =H^{\otimes n}\Ket0^{\otimes n} =(H\Ket 0)^{\otimes n} =\left(\Rsr2(\Ket0+\Ket1)\right)^{\otimes n} ={1\over\sqrt{N}}\sum_{x=0}^{N-1}\Ket x .$
Secondly, derive $U_s$ from $U_s =2\Ket s\Bra s-I =2\left(H^{\otimes n}\Ket0^{\otimes n}\Bra0^{\otimes n}H^{\otimes n}\right)-H^{\otimes n}~I~H^{\otimes n} =H^{\otimes n}\left(2\Ket0^{\otimes n}\Bra0^{\otimes n}-I\right)H^{\otimes n} .$
When $n=2,~U_s=(H\otimes H)(2\Ket{00}\Bra{00}-I)(H\otimes H).$ The middle operator is $\begin{bmatrix} 1&0&0&0\\ 0&-1&0&0\\ 0&0&-1&0\\ 0&0&0&-1\\ \end{bmatrix} =\begin{bmatrix} Z&0\\ 0&-I\\ \end{bmatrix} .$
In IBM Q Experience, the middle operator is
$(X\otimes X)(I\otimes H)cX(I\otimes H)(X\otimes X) =\begin{bmatrix}0&X\\X&0\end{bmatrix} \begin{bmatrix}H&0\\0&H\end{bmatrix} \begin{bmatrix}I&0\\0&X\end{bmatrix} \begin{bmatrix}H&0\\0&H\end{bmatrix} \begin{bmatrix}0&X\\X&0\end{bmatrix} =\begin{bmatrix}0&X\\X&0\end{bmatrix} \begin{bmatrix}HIH&0\\0&HXH\end{bmatrix} \begin{bmatrix}0&X\\X&0\end{bmatrix}\\ =\begin{bmatrix}0&X\\X&0\end{bmatrix} \begin{bmatrix}I&0\\0&Z\end{bmatrix} \begin{bmatrix}0&X\\X&0\end{bmatrix} =\begin{bmatrix}XZX&0\\0&XIX\end{bmatrix} =\begin{bmatrix}-Z&0\\0&I\end{bmatrix} \sim \begin{bmatrix} 1&0&0&0\\ 0&-1&0&0\\ 0&0&-1&0\\ 0&0&0&-1\\ \end{bmatrix} .$
Note: $XZX=-Z$.
# Initialisation
import sys
sys.path.append('../')
from qtol import *
# U_f
# To show states properly, we use the q[1]q[0] convention, having LSD on q[0].
# In other words, the control bit is MSD, which is q[1].
# When s is with control, and i on LSD, it encodes 10.
# We have ss=00, is=01, si=10, ii=11.
# Number of qubits
qbNum = 2
# Define the Quantum and Classical Registers
q = QuantumRegister(qbNum)
c = ClassicalRegister(qbNum)
# Preparation
prep = QuantumCircuit(q, c)
prep.h(q)
winning = "10"
encode = QuantumCircuit(q, c)
if (winning == "00"):
encode.s(q[1])
encode.s(q[0])
elif (winning == "01"):
encode.iden(q[1])
encode.s(q[0])
elif (winning == "10"):
encode.s(q[1])
encode.iden(q[0])
elif (winning == "11"):
encode.iden(q[1])
encode.iden(q[0])
czdesign = 2
cz = QuantumCircuit(q, c)
if (czdesign == 1):
cz.iden(q[1]) # For drawing alignment
cz.h(q[0])
cz.cx(q[1], q[0])
cz.iden(q[1]) # For drawing alignment
cz.h(q[0])
elif (czdesign == 2):
cz.iden(q[0]) # For drawing alignment
cz.h(q[1])
cz.cx(q[0], q[1])
cz.iden(q[0]) # For drawing alignment
cz.h(q[1])
u_f = encode + cz + encode
#show_me(prep + u_f, q, c, show_nice_text=True)
#circuit_drawer(prep + u_f)
# U_s and Iteration
usdesign = 1
u_s = QuantumCircuit(q, c)
if (usdesign == 1):
# Original IBM Q Experience
u_s.h(q)
u_s.x(q)
u_s += cz
u_s.x(q)
u_s.h(q)
elif (usdesign == 2):
# Replace HXH with Z
u_s.h(q[1])
u_s.x(q[1])
u_s.z(q[0])
u_s.cx(q[1], q[0])
u_s.z(q[0])
u_s.x(q[1])
u_s.h(q[1])
qc = prep
# Circuit building
# Iteration
for i in range(1):
qc += u_f + u_s
# Finalisation
# ...
show_me(qc, q, c, show_latex=True, show_histogram=True)
circuit_drawer(qc)